Introduction
Consider a classification model like the one in our previous article on Exploratory Data Analysis (EDA) that was determining whether a job is fraudulent or not. The algorithm is trained and we want to see how well it performs on a set of 10 jobs from a test set it has never seen before. Of these 10, we know for a fact that 6 are genuine job ads and that 4 are fraudulent. Our algorithm then goes ahead and classifies 3 of the jobs as fraudulent, of which 2 are actually fraudulent and 1 is a genuine job advert. Admittedly, these numbers are a bit confusing so let’s pause here for a bit and talk about a confusion matrix. We will get back to the numbers later.
Now, before we proceed, there are a few terms we will need to understand
- True Positives (TP) - the jobs that are correctly identified as fraudulent
- True Negatives (TN) - the jobs that are correctly identified as legitimate/genuine
- False positives (FP) - the genuine jobs that were incorrectly identified as fraudulent
- False Negatives (FN) - the fraudulent jobs that were incorrectly identified as legitimate.
These four terms make up a confusion matrix which is basically a table used to define the performance of a classification algorithm.
Going back to the numbers in our case, we have two true positives, five true negatives, two false negatives, and one false positive. These can be presented in a confusion matrix as shown below
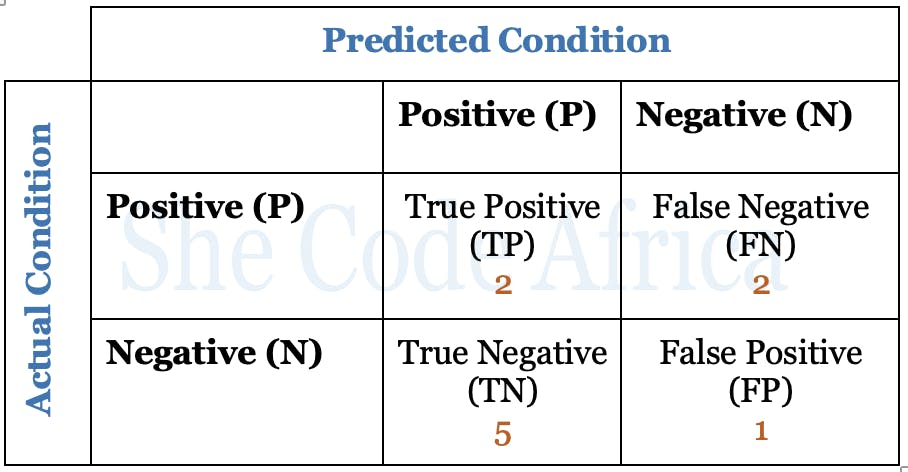
From the mathematical formula for calculating the accuracy of a machine learning model i.e the number of true positives and true negatives divided by the number of true positives, true negatives, false positives, and false negatives.
$$ Accuracy = (TP + TN) / (TP + TN + FP + FN) $$
Or to try and put it simply,
$$ Accuracy = ( No. of Correctly Classified Samples / Total No. of Samples ) $$
We find that our model achieved an accuracy score of 70% in classifying job adverts. You can learn more about the confusion matrix here . Google, in their Machine learning concepts course, also did a great job of trying to simplify the True vs False, Positive vs Negative using Aesop’s fable of The Boy Who Cried Wolf. You can check it out here as well.
It doesn’t matter that a model achieves a 0.999999 accuracy if missing a single case is enough to sabotage the entire system
So what is it?
Picture this: a group of developers guess the release date for the third instalment of Bridgerton, and whoever guesses the date which is either the exact release date or closest to the release date is the most accurate one. This degree of being closer to a set value is what we call Accuracy
In machine learning, it is a way to measure how often an algorithm classifies a data point correctly. It is the number of correctly predicted data points out of all data points and is a key aspect of evaluating the performance of any machine learning model.
Code Example
In the following section I use sklearn’s make_classification to create a random n-class classification problem. I then go ahead and create a model out of it, train it, fit it and determine its accuracy score.
Input
# importing libraries
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
# using make_classification to generate a random n-class classification problem
x, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1)
# creating and fitting the model
xtrain, xtest, ytrain, ytest = train_test_split(x, y, test_size=0.2, random_state=42)
model = LogisticRegression()
model.fit(xtrain, ytrain)
print(accuracy_score(ytest, model.predict(xtest)))
Output
0.98
Word of caution (Accuracy Paradox)
Accuracy is widely used in ML problems due to its simplicity and relative ease of implementation. However overall accuracy can be misleading when the class distribution is imbalanced, and it is extremely critical to predict the minority class correctly.
A model may have a high accuracy score but be too crude to be useful.
Take for example an algorithm set to predict cancer . We cannot afford to misdiagnose patients i.e we cannot miss malignant cases neither can we diagnose benign cases as malignant. Doing either of these erroneously could fatally result in putting healthy people through life altering treatment or declaring people cured when in fact their lives are at risk.
Taking the cancer dataset example, we could intentionally make it imbalanced by removing most of the malignant cases so only about 5.6% are malignant. Further we could use only a single feature to make our predictions. Upon checking the model’s accuracy, we find an outstanding score of 0.94736 which looks impressive until we bring forth our confusion matrix and class-level predictions, and our model falls apart by misdiagnosing almost all malignant cases.
In this case the accuracy score result is the opposite of what we expected i.e we intentionally made our model accurate at predicting wrong results. This dilemma is what is called the Accuracy Paradox, where a model gives a false premise of a high accuracy value when the dataset is highly imbalanced thus mispredicting the minority class.
For cases such as these - serious medical illnesses, terrorist attacks and economic crises etc., it doesn’t matter that a model achieves a 0.999999 accuracy if missing a single case is enough to sabotage the entire system. So what am I trying to say? Bottomline, relying on accuracy alone is not enough and can even be misleading. Fortunately, this can be mitigated by taking into consideration the specific situations and choosing other metrics to augment accuracy such as;
- Precision
- Recall
- F-Score
- Area Under Curve
- Mean Absolute Error
- Mean Squared Error
- Logarithmic Loss
Conclusion
Having looked at accuracy and its implementation, we can conclude that when classifying in predictive analytics, accuracy is not a good metric for predictive models. This is because a model may have a high accuracy score but be too crude to be useful. Care should thus be taken not to rely solely on accuracy as an evaluation metric as evidenced from the examples herein.
That has been it from me. See you on the next one. Be Safe. Be Kind. Peace.

